傅里叶级数与变换

参考资料：
[1] 通俗易懂的理解傅里叶变换（一）
[2] 傅里叶变换

傅里叶级数与变换是信号处理中的重要概念，它们可以将信号从时域转换到频域，从而更好地理解信号的特性。傅里叶级数与傅里叶变换不同：

傅里叶级数：在时域是一个周期且连续的函数，而在频域是一个非周期离散的函数。

傅里叶变换：在时域是一个非周期且连续的函数，转换为频域的一个非周期连续的函数。

傅里叶级数 Fourier series

傅里叶级数 Fourier series 直观理解就是任何周期函数都可以分解成无数个正弦函数。进一步可以分解成简单振荡波（正弦波和余弦波）。

其理论基础是三角函数的正交性，即正弦函数和余弦函数在一个周期内的积分为0。可见参考资料[2]。这些基函数的频率是整数倍的基频率，即空间中的基为。

而傅里叶级数的公式为：

其中， 为直流分量， 和 为交流分量， 为角频率。

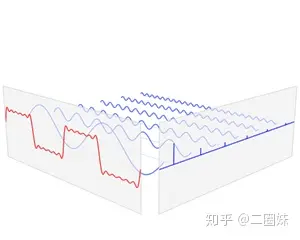
时域与频域

时域是指信号随时间变化的情况，频域是指信号随频率变化的情况。傅里叶级数可以将时域的信号转换到频域，即将信号分解成一系列的正弦函数。

傅里叶变换 Fourier transform

傅里叶变换是傅里叶级数的推广，它允许我们将一个非周期函数转换为频率域表示。这个过程是可逆的，即可以通过逆傅里叶变换从频率域回到时间域。

一个简单的看法就是我们把非周期函数的周期看成无穷大。

具体分析变化参见参考资料[1]。